A Crosstab report (aka Contingency Table) allows you to cross tabulate at least two questions, one or more in the columns (also known as banner questions) and one or more in the rows (also known as stubs). Use Crosstabs to examine trends and patterns that are driving your summary results.
Answer grouping and question nesting are only available for Alchemer customers on enterprise plans. If you are interested in upgrading to an enterprise plan, please reach out to Alchemer Sales.

Compatible Question Types
- Radio Button
- Checkboxes
- Dropdown Menu (Single)
- Image Select (Single)
- Image Select (Multiple)
- Rating (Likert Scale)
- NPS®
- Radio Button Grid Rows
- Checkbox Grid Rows
- URL Variables
- SSO Variables
Setup
1. Go to Results > Reports
2. Click Create Report > Crosstab.
3. Give your report a Title.
4. Add Your Columns, also known as Banners. To add multiple questions, simply select them one after another. Delete any answer options from the list below that you do not wish to include.
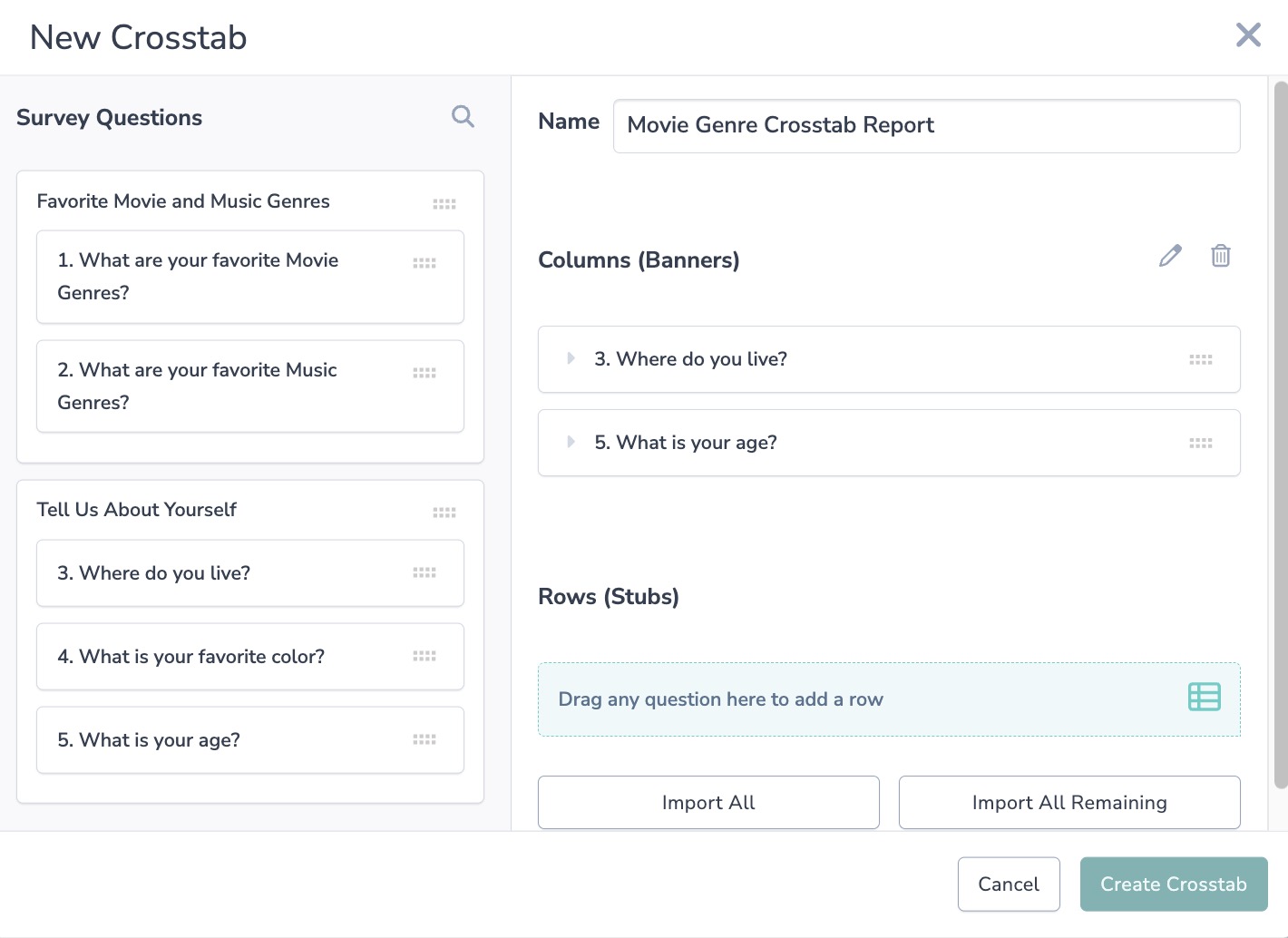
5. Next, add your Rows (aka Stubs).
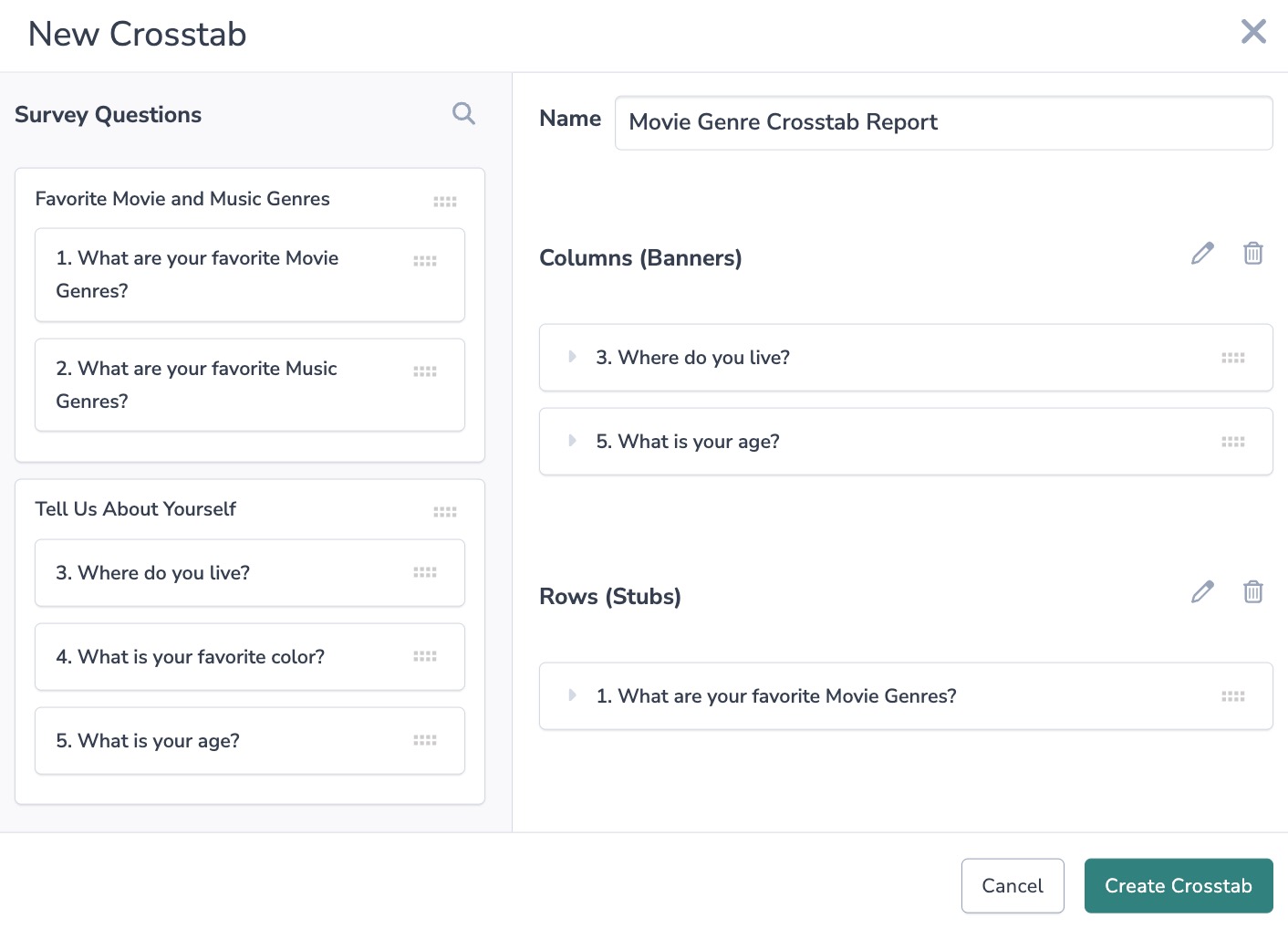
6. Once you've added your Columns and Rows, click "Create Crosstab".
Crosstab Options
After creating your crosstab, there are a series of Cell Content, Statistical, and Heatmap options to choose from.
There are two ways to access these options"
- Click on Cell & Statistics for your crosstab report element.
OR - Click Report Options > Crosstab
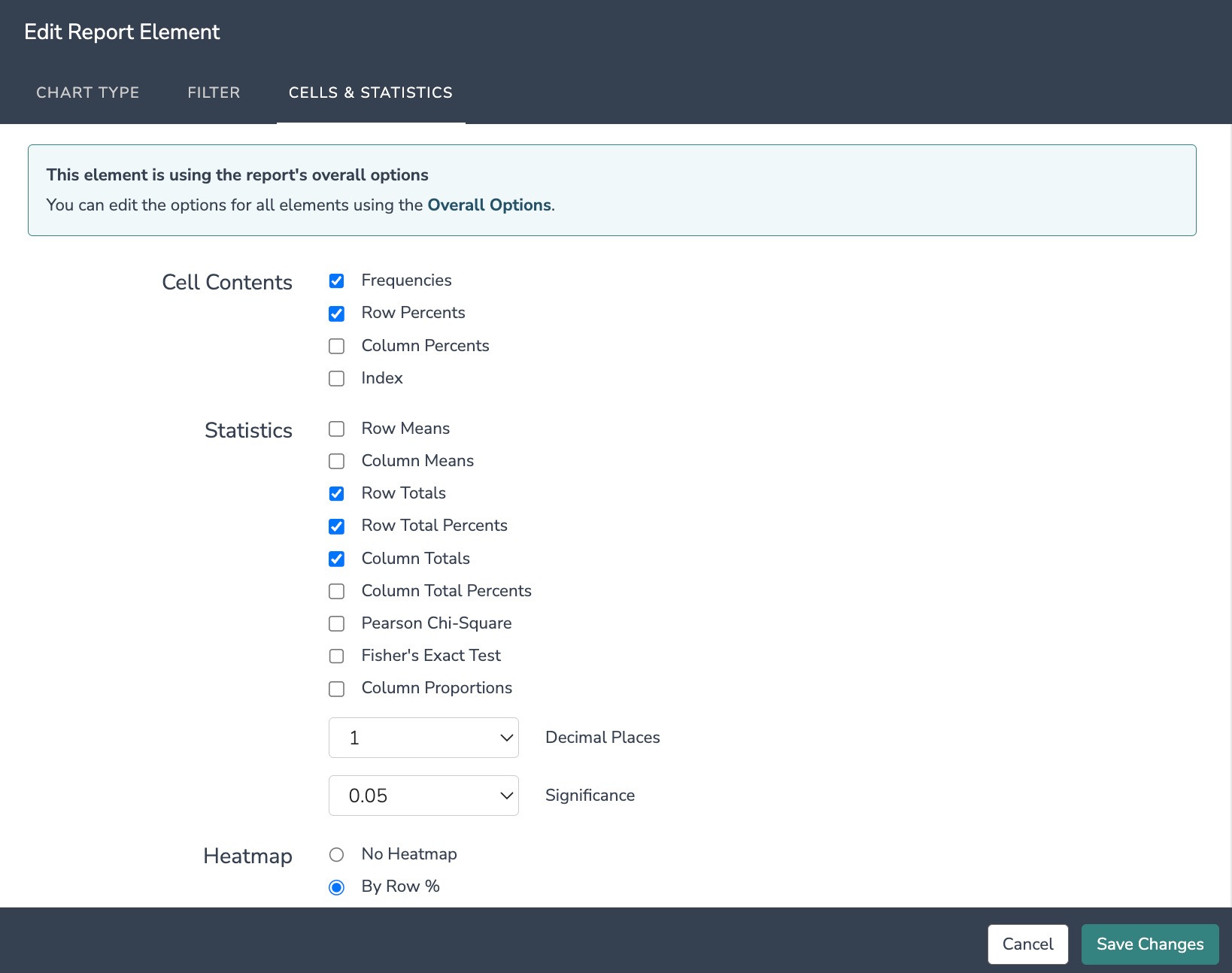
Frequencies - These are just the counts of responses. Check out the Understanding Crosstab Totals section of this tutorial to learn more.
Row Percents - Row percents are computed by taking the cell count divided by the row total. Check out the Understanding Row and Column Percents section of this tutorial to learn more.
Column Percents - Column percents are computed by taking the cell count divided by the column total. Check out the Calculating Row and Column Percents section of this tutorial to learn more.
Index - The index is the likelihood of having both the row and column characteristic in comparison to the base population. The Index is calculated by dividing either the Row % in the cell by the Column Total % or by dividing Column % in the cell by the Row Total %. Either calculation generates the same result. Check out the Calculating the Index section of this tutorial to learn more.
Row Means - The row mean can be computed when the banner (the question in the column) has numeric reporting values; otherwise row means are not available. Check out the Calculating Row and Column Means section of this tutorial to learn more.
Row Means are not available for answer grouping and nested questions.
Column Means - The column mean can be computed when the stub (the question in the row) has numeric reporting values; otherwise column means are not available. Check out the Calculating Row and Column Means section of this tutorial to learn more.
Column Means are not available for answer grouping and nested questions.
Row Totals - For single select questions, the row total is the total number of responses for all shown answer options in the crosstab. For multi-select questions, the row total is the total number of respondents who selected at least one of the shown answer options in the crosstab. Check out the Understanding Crosstab Totals section of this tutorial to learn more.
NOTE: The row total may be different than the sum of boxes checked in the row question because multi-select questions allow a single respondent to select more than one answer option.
Column Totals - For single select questions, the column total is the total number of responses for all shown answer options in the crosstab. For multi-select questions, the column total is the total number of respondents who selected at least one of the shown answer options in the crosstab. Check out the Understanding Crosstab Totals section of this tutorial to learn more.
NOTE: The column total may be different than the sum of boxes checked in the column question because multi-select questions allow a single respondent to select more than one answer option.
Pearson Chi-Square - The chi-square (X²) statistic is used to investigate whether the data from two questions are correlated. The Pearson's Chi-Square test will assess whether the two cross-tabulated questions are independent or unrelated. A significant chi-square means that the data is related. Check out the Chi-Square section of this tutorial to learn more.
Fisher's Exact Test - Fisher's Exact Test is only available for analyzing 2x2 tables, meaning the cross tabulation of two questions each with only two answer options. Fisher's test is the best choice when available as it always gives the exact P value, while the chi-square test only calculates an approximate P-value. Fisher's is typically employed when sample sizes are small, but it is valid for all sample sizes. Check out the Fisher's Exact Test section of this tutorial to learn more.
Column Proportions - This significance test analyzes all pairs of columns by row within a given banner question. If a given cross tabulation of two questions are found to be significantly related (based on the results of the Chi-Square test) you can use the column proportions test to look at the rows and compare pairs of columns, to test whether the proportion of respondents in one column is significantly different from the proportion in the other column. The proportion is the count in the cell divided by the total for the column. Check out the Column Proportions section of this tutorial to learn more.
Notes:
- When selecting Column proportion significance testing, the Heatmap option will be toggled off; you can change this setting back if you wish.
- Column proportions are only run on cross-tabulated questions that have a significant Chi-Squared on your specified significance level).
Decimal Places - Customize the decimal places displayed to either 0, 1, or 2.
Significance - Choose the confidence level (0.10, 0.05, or 0.01) for your significance testing (both Chi-square and Column Proportions).
Heatmap - Heat mapping will highlight the cells in a range of color shades – darker for higher numbers and lighter for lower numbers. There are four heatmap options: no heatmap, by the row %, by column %, or by index.
Note: The Heatmap option will be toggled off when selecting Column proportion significance testing; you can change this setting back if you wish.
Answer Grouping and Question Nesting
Answer grouping and question nesting functionality is only available for Alchemer customers on enterprise plans. If you are interested in upgrading to an enterprise plan, please reach out to Alchemer Sales.
Answer Grouping
When building crosstab reports, you can group answer options together. You can add answer grouping when creating a new crosstab report or when you edit an existing crosstab report by clicking Columns and Rows.
In the example video below, instead of listing every city as its column row, the East Coast cities are grouped under one East Coast column, likewise with the West Coast cities.

Question Nesting
When building crosstab reports, you can also nest a question under another question.
You are limited to one layer of question nesting.
In the crosstab builder, simply drag a question under the right side of another question.

Understanding Crosstab Totals
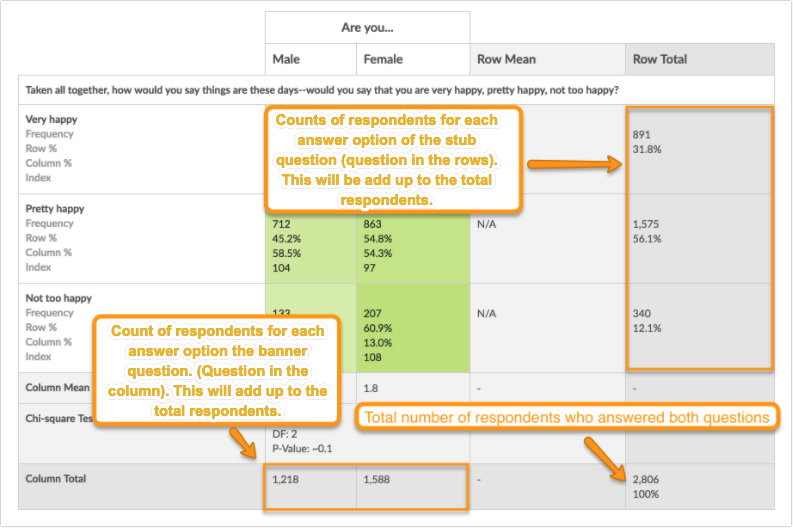
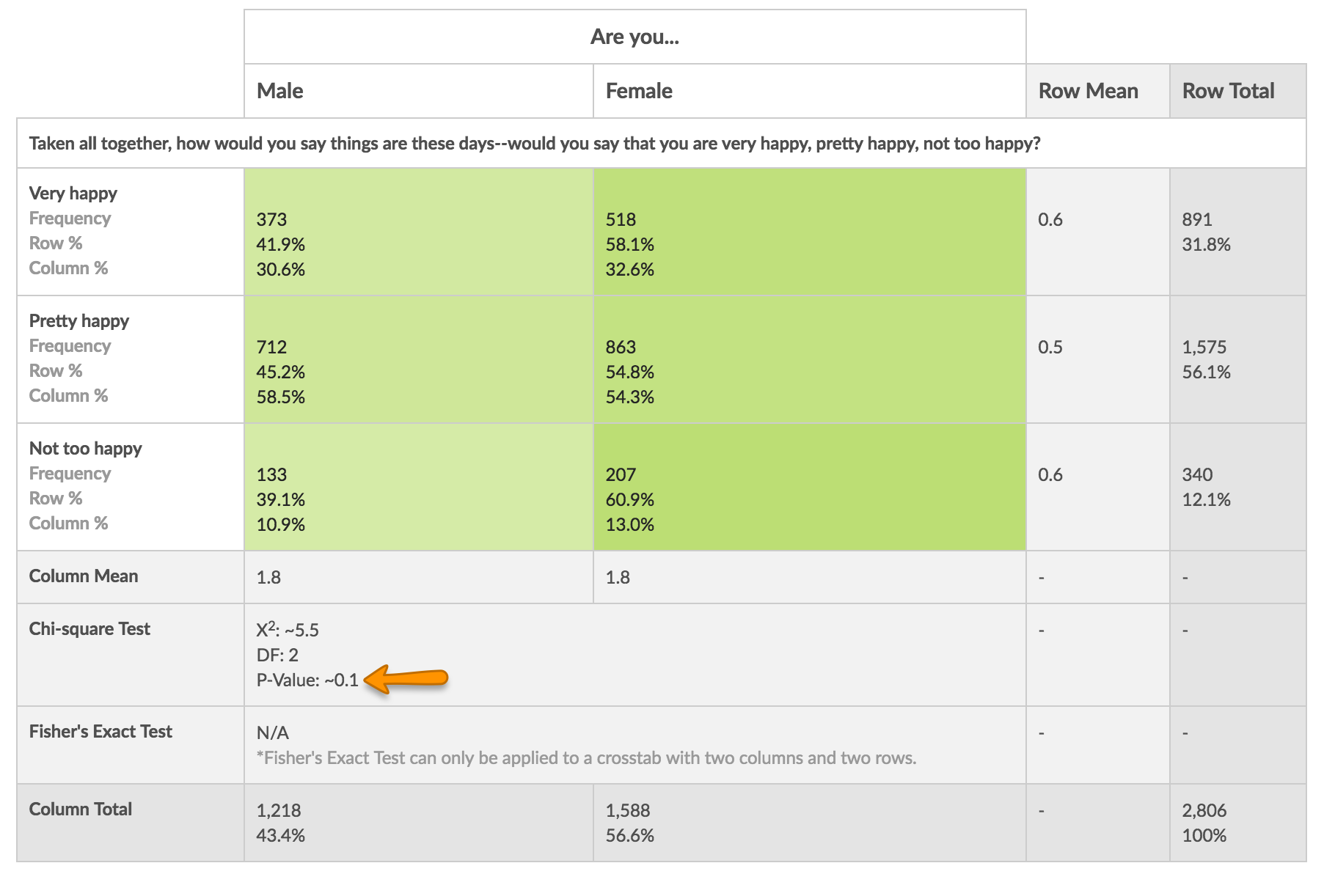
Below you'll see that 2,806 people answered both the happiness question and the gender question as crosstabs are subset to responses that have an answer for both questions.
To the left of the 2,806, across the horizontal, you'll have a count for responses that selected each answer option for the Banner question (the question in the columns).
Of the 2,806 respondents who responded to these questions 1,218 are Male and 1,588 are Female. These will add up to the total number of responses: 1,218 + 1,588 = 2,806.
Above the 2,806, you'll have the count for each of the answer options for the question in the rows (aka Stubs).
Of the 2,806 respondents who responded to these questions, 891 are Very happy, 1,575 are Pretty happy, and 340 are Not too happy. These will also add up to the total number of responses: 891 + 1,575 + 340 = 2,806.
Understanding Row and Column Percentages
The Row % is the percentage of total people defined in the row who also have the column characteristic. It is computed by dividing the cell total by the row total.
In the below example 41.9% of Very happy respondents are also Male.
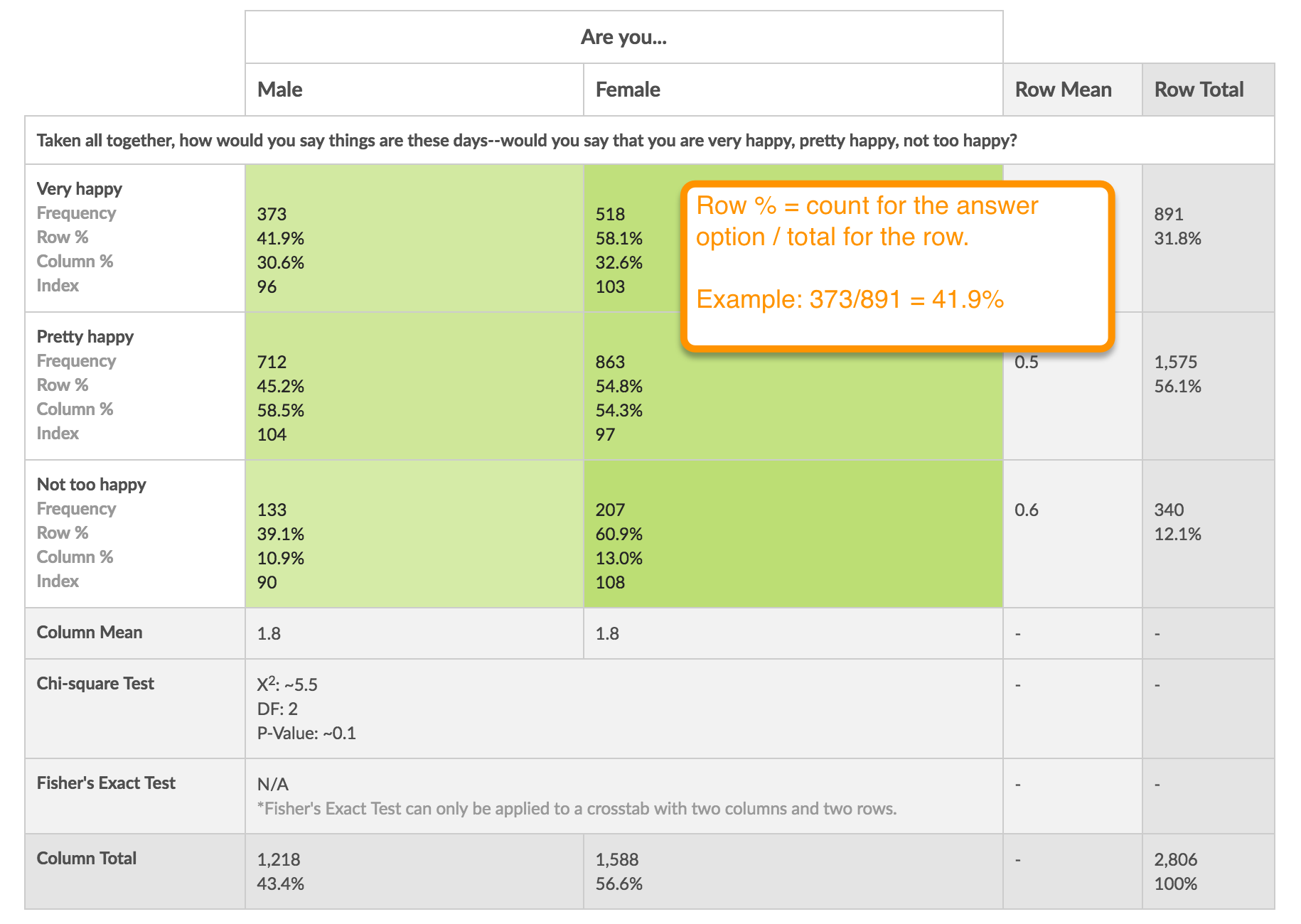
By default, the Crosstab will display a Row % in each cell. If you wish to display column percentages, toggle this option on setup or edit the Crosstab and click Override Global Report Styles to see the Cell Contents options.
The Column % is the percentage of total people defined in the column who also have the row characteristic. It is computed by dividing the cell total by the column total.
In the example below 32.6% of Female respondents are also Very happy.
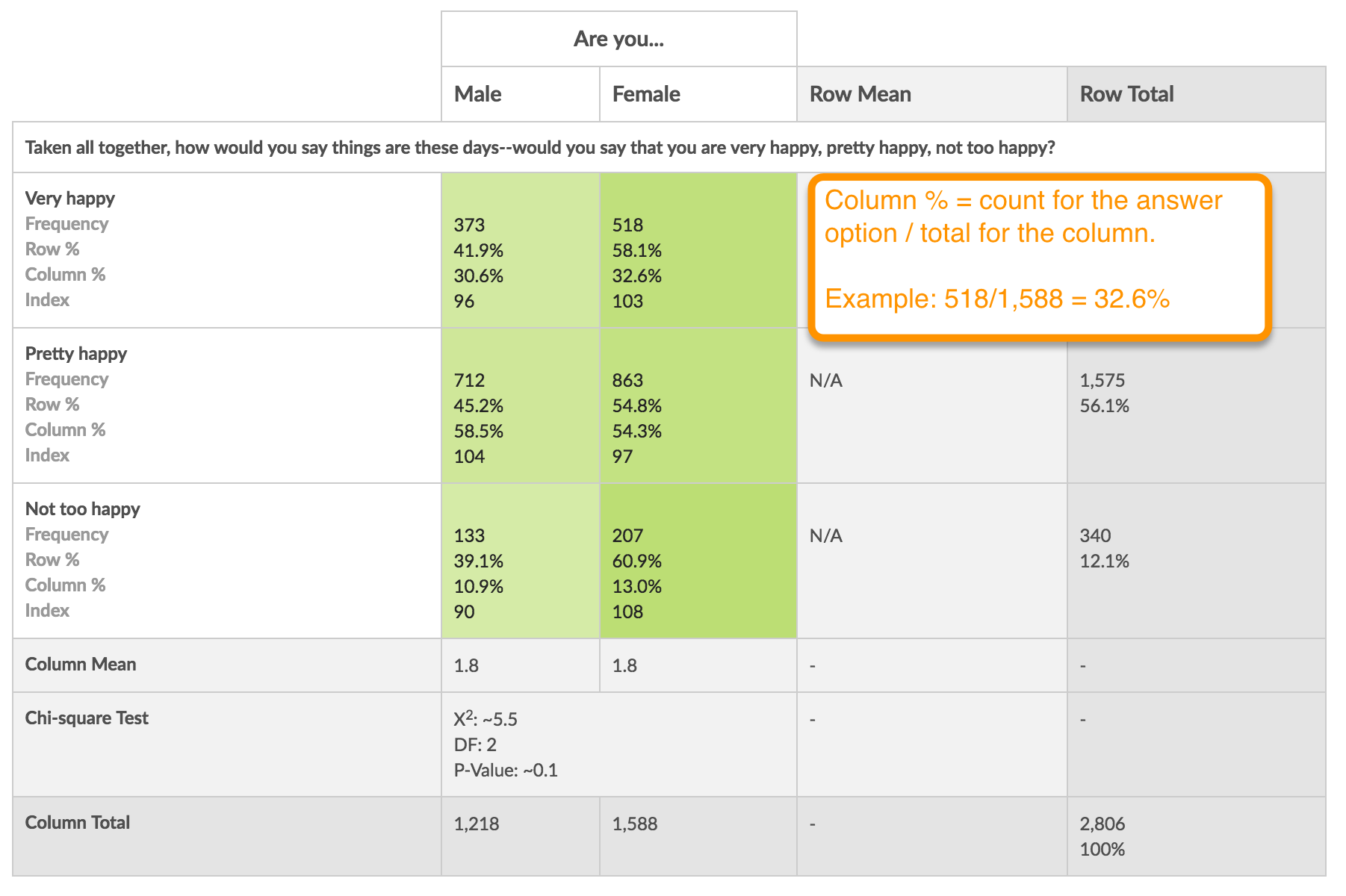
Understanding the Index
By default, the Crosstab will display a Row % in each cell. If you wish to display an index, toggle this option on setup or edit the Crosstab and click Override Global Report Styles to see the Cell Contents options.
The index is the likelihood of having both the row and column characteristic in comparison to the base population.
Indices are computed by dividing the Row % for the cell by the Column Total % or the Column % for the cell by Row Total %; these number will be identical. This value is then multiplied by 100.
Indices over 100 indicate a higher likelihood and indices under 100 indicate a lower likelihood.
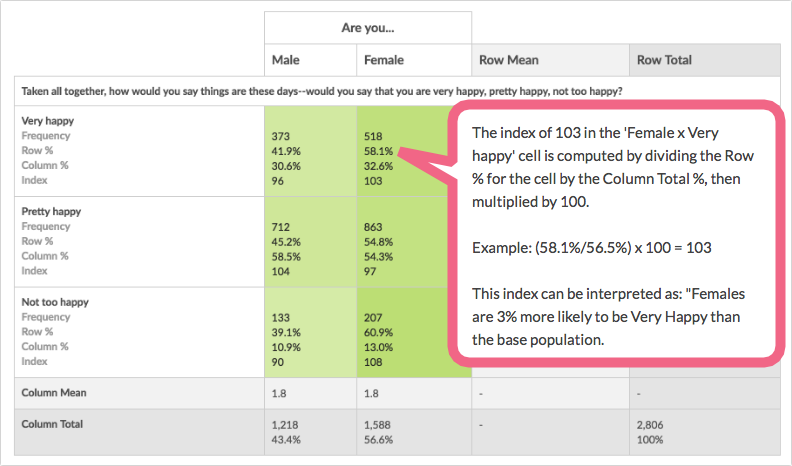
In the below example, the index of 103 in the Female x Very happy cell means that Females are 3% more likely to be Very happy than the base population. Similarly, the index of 96 in the Male x Very happy cell means that Males are 4% less likely to be Very happy than the base population.
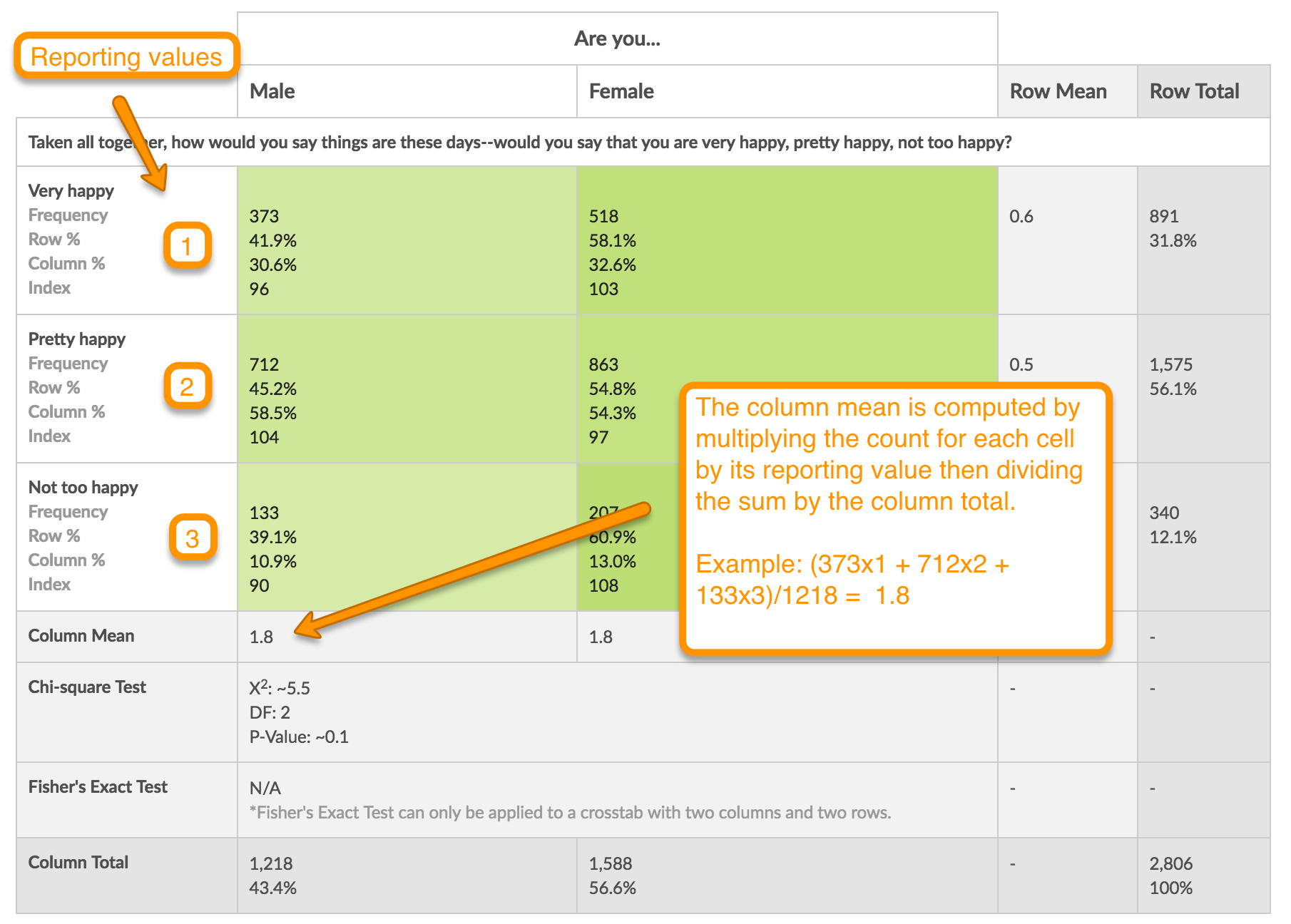
Understanding Row and Column Means
Row and Column means are calculated when numeric reporting values are present. The row mean can be computed when the banner (the question in the column) has numeric reporting values; otherwise, row means are not available. The column mean can be computed when the stub (the question in the row) has numeric reporting values; otherwise, column means are not available.
The row mean is computed by multiplying the count for each cell by the reporting value for the answer option in the column then dividing the sum of these values by the row total.
Similarly, the column mean is computed by multiplying the count for each cell by the reporting value for the answer option in the row then dividing the sum of these values by the column total.
In the below example, the column mean is computed as follows: ((373 x 1) + (712 x 2) + (133 x 3)) / 1218 = 1.8.
When comparing the column means for Males and Females we can see that there is not much difference in happiness overall for the two groups.
Understanding Pearson's Chi Square
The chi-square (X²) statistic is used to investigate whether the data from two questions are correlated. The Pearson's chi-squared test will assess both goodness of fit and independence. Goodness of fit determines whether the distribution of your data differs from what is considered a normal distribution that would theoretically be observed in the general population if we got a response from everyone. Independence means that when the data is cross-tabulated it is unrelated or "independent."
When you run a crosstab, Alchemer will return a Pearson Chi-Square, Degrees of Freedom and a p-Value.
What are all these values?
- Pearson Chi-Square - The sum of squared deviations between observed (your data) and theoretical frequencies (population data).
- DF - The Degrees of Freedom is the number of values in the final calculation of the chi-square statistic that are free to vary, which is the number of categories reduced by the number of parameters calculated as (columns -1)(rows-1).
- P-Value - The level of confidence that there is a statistical difference between the distribution of your data and the theoretical distribution of data (the population). In other words, whether the two questions in your crosstab are correlated.
The DF and the P-Value are used to look up whether your Chi-square statistic is greater than the critical value of Chi Square in a Chi-Square Distribution Table: Chi-square-table.pdf
In the example we've been using in this tutorial, we have cross-tabulated gender and happiness because we expect that they may be correlated. In the chi-square test below the important number to check is the P-Value. As you can see, the p-Value is 0.1 which means the two questions are correlated at the 0.1 significance level but not the more stringent 0.05 or 0.01 levels.
Understanding Fisher's Exact Test
Fisher's Exact Test is available for 2x2 Crosstabs, meaning the cross tabulation of two questions each with only two answer options. Fisher's test is the best choice when available as it always gives the exact P value, while the chi-square test only calculates an approximate P value. Fisher's is typically employed when sample sizes are small, but it is valid for all sample sizes.
Depending on the significance you choose (0.1, 0.05, or 0.01), a P-value value that is less than or equal to your significance level indicates that there is an association between the two classifications you are examining.
Understanding Column Proportion Testing
Notes:
- When selecting Column proportion significance testing, the Heatmap option will be toggled off; you can change this setting back if you wish.
- Column proportions are only run on cross-tabulated questions that have a significant Chi-Squared on your specified significance level).
If a given cross tabulation of two questions is found to be significantly related (based on the results of the Chi-Square test) you can use the column proportions compare pairs of columns by row, to test whether the proportion of respondents in one column is statistically different from the proportion in the other column. The proportion being the count in the cell divided by the total for the column.
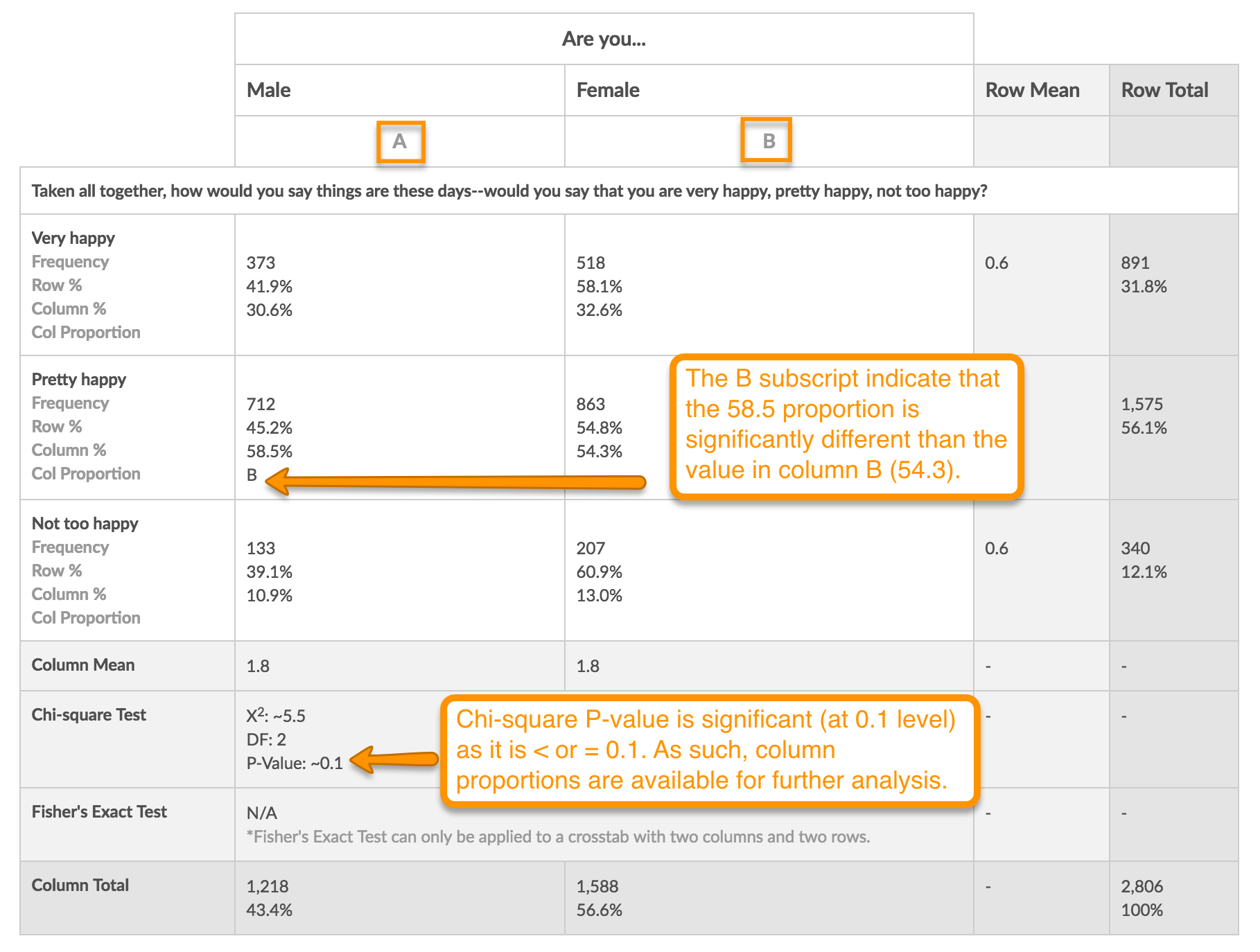
For example, after using a chi-square test to find that Happiness and Gender are not independent (at the 0.1 significance level), you may want to dig in to see which cells are responsible for this relationship.
When you add the Column Proportion test to your crosstab each column will receive letters as keys. All column pairs within a significant banner question (as determined by the Chi-square test) will be compared against each other by row. Significant differences in Column % will be notated with a subscript letter that corresponds to the column's key. The letter that is displayed and the column it is placed in are determined based on the column %; whichever column % is higher will receive the subscript letter. The letter that is displayed is the column for which that column % is significantly different.
In the below example, the Pretty happy x Male cell has a subscript of B, which indicates that its column % (58.5%) is significantly higher than that of column B (54.3%).
Net Promoter®, NPS®, NPS Prism®, and the NPS-related emoticons are registered trademarks of Bain & Company, Inc., Satmetrix Systems, Inc., and Fred Reichheld. Net Promoter Score℠ and Net Promoter System℠ are service marks of Bain & Company, Inc., Satmetrix Systems, Inc., and Fred Reichheld.